For MHz oscillating crystals, the so-called "fundamental oscillation" (fundamental oscillation) or a harmonic (usually the third or fifth harmonic) is used. The decisive factor here is the mechanical mode of vibration of the quartz crystal, which is based on the piezoelectric effect of quartz. In the MHz range, the fundamental mode (available from PETERMANN-TECHNIK GmbH up to 285 MHz) is typically used in thethickness-shear mode.
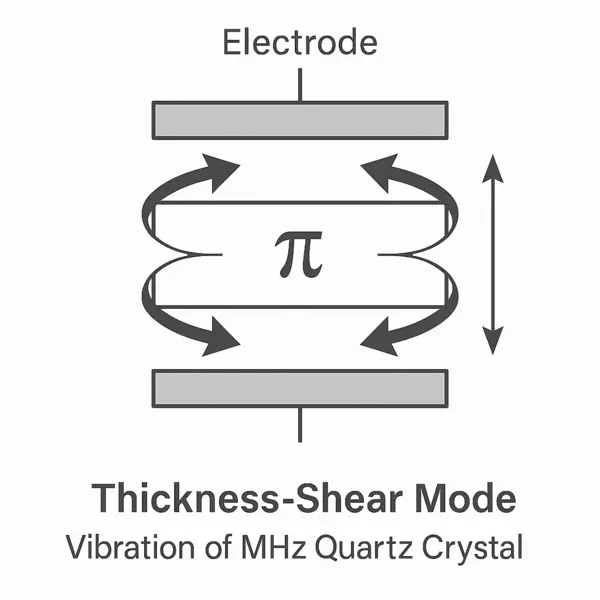
Oscillation mode in the MHz range: Thickness shear oscillator (planar shear mode)
What happens in the process?
The quartz crystal is ground and cut (usually AT cut) in such a way that it oscillates in a certain thrust mode when an alternating voltage in the MHz range is applied. The quartz does not move in the longitudinal direction or transversely to the surface, but the oscillation takes place in the plane of the crystal, i.e. like a lateral "shearing".
The resulting movement is reminiscent of two plates lying on top of each other and being displaced against each other - this is the "shearing" movement.
How it works in detail
- AT cut:
- The quartz crystal is cut at a specific angle to the crystal axis (approximately 35°15' to the Z-axis).
- This special cut produces the desired oscillation shape (shear mode) and ensures temperature stability in the MHz range.
- Application of an alternating voltage:
- Electrodes on both sides of the quartz generate an electric field through the crystal.
- Due to the piezoelectric effect, the crystal deforms mechanically (it begins to vibrate) as soon as a voltage is applied.
- The mechanical oscillation in turn generates an electrical voltage - a self-reinforcing effect at the resonance frequency.
- Resonance in the MHz range:
- The thickness of the quartz crystal determines the resonance frequency (at 10 MHz, for example, the thickness is approx. 0.33 mm).
- The fundamental frequency is the lowest possible natural frequency at which the quartz resonates in shear mode.
Why this particular form of vibration?
Reason | Explanation |
Good frequency stability | AT section has a flat temperature frequency behaviour at room temperature up to approx. 70 °C. |
Efficient energy transfer | The shear mode couples well with the electric field and loses little energy. |
Low attenuation in the MHz range | The oscillation is mechanically stable and has a high quality factor (Q factor). |
Small size possible | The thickness-frequency relationship allows high frequencies to be realised with thin quartz. |
Alternatives: Harmonic operation
Some crystals in the higher MHz range (e.g. 30 MHz, 50 MHz) use the 3rd or 5th harmonic of the same oscillation mode. They therefore oscillate at a multiple of the fundamental frequency.
Why?
- The manufacture of very thin quartz crystals for high fundamental frequencies is mechanically difficult.
- Instead, thicker crystals are used on a higher harmonic - easier to manufacture, but requiring special circuits.
Conclusion
In the MHz range , the fundamental oscillation is used in the thickness shear oscillation mode because it:
high frequency stability,
good quality (low losses),
insensitivity to temperature,
and efficient electrical coupling.
These properties make it ideal for precise clock generators, which are used today in all applications in the electronics sector.
A note on our own behalf: Due to our fundamental resonator designs, we can supply fundamental frequencies of up to 285 MHz - see here: https://www.petermann-technik.de/produkte/quarz-konfigurator.html.
FAQs
Which oscillation mode is typically used for MHz quartz crystals?
MHz quartz crystals typically use the fundamental mode or, at higher frequencies, a harmonic, usually the third or fifth. The relevant mechanical mode of vibration is the planar shear mode, also known as the thickness shear mode. In this mode, the quartz crystal does not vibrate longitudinally or perpendicular to the surface, but in its plane as in a lateral shear motion. This oscillation mode is based on the piezoelectric effect of quartz and is particularly suitable for the MHz range. It offers high frequency stability, low losses and efficient electrical coupling.
Why is the Thickness Shear Mode particularly suitable for MHz crystals?
The thickness-shear mode is particularly suitable for MHz crystals because it enables mechanically stable and low-loss oscillation. The shear movement within the crystal plane achieves a high Q-factor. At the same time, this mode couples very well with the electric field that is applied to the quartz via the electrodes. This improves energy transfer and supports clean resonance behavior in the MHz range. This oscillation mode is therefore ideal for precise clock generators in electronic applications.
What role does the AT cut play in MHz oscillating crystals?
The AT cut is crucial for MHz quartz crystals because it significantly determines the desired oscillation shape and the temperature behavior of the quartz. The quartz crystal is cut at a defined angle of around 35°15' to the Z-axis. This special cut creates the shear mode and ensures a flat temperature frequency behavior in the range from room temperature to around 70 °C. As a result, the frequency remains particularly stable over typical operating temperatures. The AT cut is therefore the preferred standard for many industrial and electronic applications.
When are fundamental and harmonics used in MHz quartz crystals?
The fundamental frequency is the lowest natural frequency at which the quartz resonates in shear mode and is very frequently used in the MHz range. With increasing frequencies, however, the manufacture of extremely thin quartz crystals becomes increasingly challenging mechanically. For this reason, the third or fifth harmonic of the same oscillation mode is often used at higher MHz ranges. The crystal then oscillates at a multiple of its fundamental frequency, which makes it easier to manufacture thicker and more robust resonators. However, specially designed circuits are required to operate such harmonic crystals.
How does the thickness of the quartz crystal influence the resonant frequency in the MHz range?
The thickness of the quartz crystal is directly related to its resonance frequency in the MHz range. The thinner the quartz crystal, the higher the achievable fundamental frequency. At a frequency of 10 MHz, for example, the thickness of the quartz crystal is around 0.33 mm. This thickness-frequency relationship enables compact designs and high frequencies with correspondingly thin crystals. However, if very high base frequencies are required, the mechanical manufacturing effort increases significantly, which is why harmonics are often used as an alternative.
Why PETERMANN-TECHNIK vibration modes for MHz quartz crystals?
PETERMANN-TECHNIK is a strong choice for oscillation modes for MHz oscillating crystals because the company combines in-depth expertise in frequency technology with practical solutions. Based on fundamental resonator designs, fundamental frequencies of up to 285 MHz are available, which opens up an exceptionally wide range of applications. The company focuses on the technically precise design of quartz crystals in the appropriate oscillation mode, especially in the proven Thickness Shear Mode. Customers benefit from competent advice from frequency experts and a clear focus on stable, low-loss and temperature-suitable solutions. This makes PETERMANN-TECHNIK a reliable partner for demanding clock and frequency applications in the electronics sector.
